1. 평균(mean)
평균(mean)은 마치... 미분적분학을 배우기 전에 알아야 할 덧셈 뺄셈 수준이랄까..?
통계학을 제대로 배우기 전에 알아야 할 것은 바로바로 평균이다.
표본 평균 / 모집단 평균을 구하는 식은 아래와 같다

그렇군.... 평균은 만능인건가?응 아니야
특이하게 작거나 큰 값(이상치)가 자료에 들어있으면 평균값은 대푯값이 될 수 없다
마치 대선에 나갔지만 여러 전과가 밝혀져서 해당 대선의원은 대표로써 부적절한 경우라고 생각하면 될까?

2. 중앙값(median)
자료를 오름차순으로 정렬했을 때, 가운데에 위치하는 값
1) 자료가 홀수일 때
ex) [1 2 3 4 5] 에서의 중앙값은 3이다
2) 자료가 짝수일 때
ex) [1 2 3 4 5 6] 에서의 중앙값은
(3+4)/2 =3.5 이다

중앙값에 대한 식으로 나타내면 아래와 같다

3. 최빈값(mode)
자료 중에 빈도수가 최대인 값
ex) [1 1 2 3 4 5] 에서 최빈값은 1이다
ex) [2 3 3 3 4 5] 에서 최빈값은 3이다
명목자료의 경우에는 평균과 중앙값은 의미가 없으므로 최빈값을 사용한다
ex) 올해의 유행 옷 색깔
연속형 자료인 경우에는, 도수분포표 상에서 빈도가 최대인 계급의 중앙값이 최빈값이 됨

최빈값이 유용할 때?
한 의류매장에서 어느날 판매된 남성복 바지들의 허리 Size는 다음과 같았다
: 28 30 31 32 33 34 34 36 38 40
여기서 중앙값은 자료의 총 개수가 짝수이기 때문에
(33+34) / 2 = 33.5
중앙값은 33.5
최빈값은 34이다.
이 때 자료의 중심위치는 중앙값(33.5) 보다 최빈값(34) 으로 하는게 더 상식적이다.

4. 평균 & 중앙값 & 최빈값에 대한 왜도

5. 사분위수(Quartile)
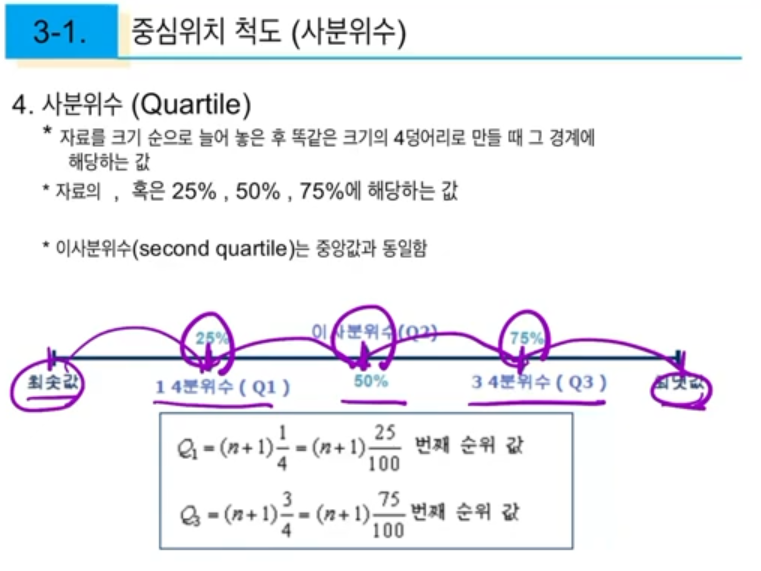
최솟값 Q1 Q2 Q3 최댓값을 4분위한 것인데
Q1(일4분위수)
Q2(이4분위수)
Q3(삼4분위수) 라고 부른다
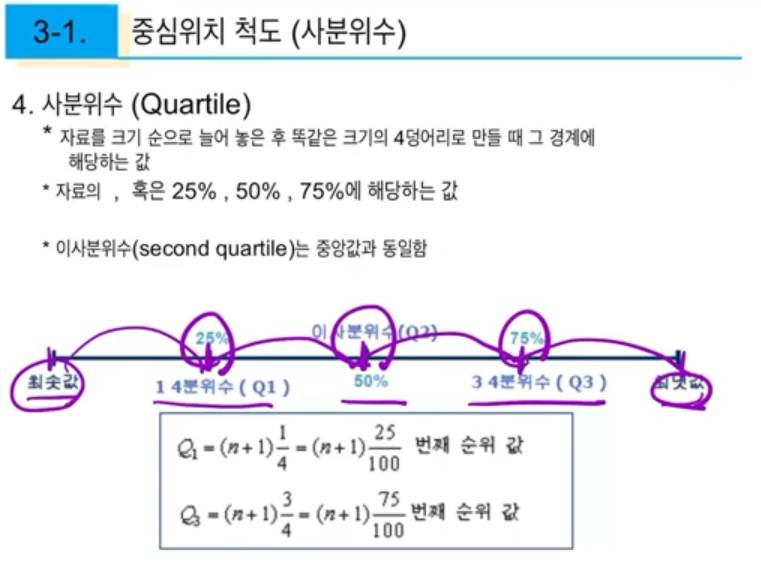
아래는 사분위수를 구하는 공식이다

예제를 보자
해당 예제에서 중앙값은 Q2와 같다는 것을 알 수 있다

다음은 Q1 Q2 Q3의 자리값과 실제값을 구하는 식이다
Q1은 2.25번째 자리값과 2.25의 실제값을 가지고 있다
Q2는 4.5번째 자리값과 4.5의 실제값을 가지고 있다
Q3는 6.75번째 자리값과 7.5의 실제값을 가지고 있다
따라서 Q1,Q2,Q3는 자리에 따른 데이터이기 때문에 자리에 대한 데이터가 실제 데이터에 없을 수 있다는 것을 유의하자
말 그대로 사분위수, 즉 4분위로 잘라놓은 자리의 값을 구하는 것이기 때문에 실제 데이터가 없는 것은 당연지사이다.

마무리이며 IQR은 추후에 공부하도록 하겠다.

'Statistics > 통계학 입문' 카테고리의 다른 글
| 특이값과 Z-Score (0) | 2022.09.30 |
|---|---|
| 변동성 척도(4분위수를 배운 이유) (0) | 2022.09.18 |
| basic - 표와 그래프(2) 줄기 잎 전시 ~ 특이값 (0) | 2022.09.05 |
| basic - 표와 그래프(1) 도수분포표 ~ 히스토그램 (0) | 2022.09.05 |
| Basic - 통계학 정의, 표본과 모집단, 자료의 종류 및 계층 (0) | 2022.09.05 |



