1. 표본공간
표본공간이 뭐냐하면, 실험에 대한 공간이라고 생각하면 된다.
이해가 안된다면 예시를 들어보자
동전의 표본공간은 뭘까?
(앞, 뒤) 이다
그러면 주사위의 표본공간은?
(1, 2, 3, 4, 5, 6)이다

여기서 잠깐! 확률에 대한 접근 방식?
확률에 대한 접근은 크게 두 가지로 나뉘는데, 바로 상대적 비율 접근 방법과, 주관적 접근 방법이다.

우리가 기본적으로 접근하는 것은 상대적 비율 접근이다.
즉 사건이 일어날 확률을 수열로 계속 나타내어 그 수열이 수렴하는 값을 그 사건의 확률로 정의하는 것을 뜻한다
말로는 이해가 안 될 수 있으니, 사진을 통해 알아보겠다.
빈도론자(상대적 비율 접근 우호) = 많이 해보면 그렇게 되더라

이제 진짜로 확률에 대해 알아보겠다.
2. 확률의 규칙
"암기했다면 살아남은 것" (필수 암기)
공리, 여러가지 규칙은 암기해야 한다.
목차
1) 확률의 공리
2) 확률의 규칙
3) 상호배반과 독립
4) 결합확률, 주변확률
5) 조건부 확률, 독립
1) 확률의 공리
THM
1. 간단하게 표본공간에서 각각의 사건의 확률은 0과 1 사이에 존재한다
2. 0과 1 사이에 존재하는 각각의 사건의 확률은 모두 합하면 1이된다
이 두 가지의 공리를 만족한다면 확률이라고 한다.

2) 확률의 규칙
규칙을 모르면 이후에 아무것도 할 수 없으니 외워야한다.

3 ) 상호배반과 독립
상호배반? 독립?
이 두 가지의 개념은 비슷해보이지만 매우 다르기 때문에 알고 넘어가야한다
일단 독립은 이후에 나오기 때문에 지금은 설명하지 않고
상호배반에 대하여 설명하겠다.
쉽게 말하자면 상호배반은 사건 A와 B가 있을 때 교집합이 없는 사건을 상호배반이라 한다.
즉 반대로 말하자면 상호배반인가? 상호배반이 아닌가?에 대한 여부를 알고 싶으면
다음과 같이 상호배반 사건의 합 규칙을 사용해보면 알 수 있을 것이다.

4) 결합확률, 주변확률

결합확률: 교집합의 확률
주변확률: 두 개의 변수를 동시에 고려하는 상황에서 어느 한쪽만을 생각할 때의 확률
주변확률에 대해서 더 자세히 알아보자
주변확률은 동시에 일어나는 확률에 대해서 한가지 상황에 포커싱을 두고 계산하는 확률이다.
구하는 방법은 다음 사진처럼 구하면 된다.

5) 조건부 확률, 독립
#1 조건부 확률의 공식은 무조건 외워야 한다. 이후 베이즈 정리에서 매우 많이 나오기 때문!!
학점이 좋은 학생의 취업 확률은 이렇게 나타낼 수 있다.
P(취업 | 학점 좋음)
반대로 학점이 낮은 학생의 취업 확률은 이렇게 나타낼 수 있다.
P (취업 | 학점 낮음)

위에서 배운 조건부 확률 공식을 이용하여 예제를 풀어보자
예제) 카드놀이에서 빨강색 카드를 뽑았을 때 그 카드가 에이스일 확률은?
조건부 확률 공식을 이용하여 풀어보면 답은 2/26이 나온다

주사위 2개를 동시에 던졌을 때, 사건 A가 일어난 상태에서 사건 B를 만족하는 조건부 확률을 구하는 방식은
다음과 같다.

다음은 조건부 확률의 곱셈규칙이다. 이 부분 또한 매우 중요하여 암기를 무조건 해야한다.

#2 독립
독립은 어느 사건이 다른 사건과 일어날 확률이 무관할 때를 뜻한다.
예를 들어
A: 동전
B: 주사위
라고 한다면 동전과 주사위의 숫자는 서로 무관하다.
즉 조건이 확률에 미치는 영향이 없다 !!
이것을 독립이라고 한다
추가로 독립인지 아닌지 어떻게 아냐고 물으신다면,,,
바로....
아래와 같이 독립 공식을 만족할 때 독립이라고 합니다 .. ㅎ

아래는 독립의 예시이다
남성과 여성에 따라 승진 여부에 대해 차이를 보이고 있는지를 확인하기 위하여
사건 A: 남성
사건 B : 승진함
조건부 확률 P(A | B)라고 둘 수 있다.
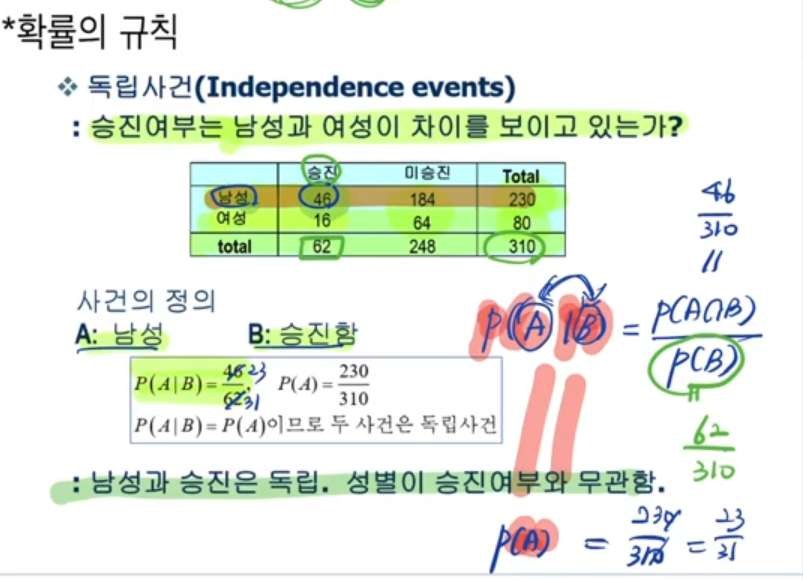
독립 사건의 곱셈 규칙은 다음과 같다

독립인지 아닌지에 대해 알기 위해서
S = { HH, HT, TH, TT } 로 두고
독립 곱셈규칙을 적용했을 때
독립 곱셈 규칙을 만족하지 않기 떄문에
독립이 아니라는 결론을 내릴 수 있다 !

다음은 베이즈 정리에 대하여 정리해보겠습니당
'Statistics > 통계학 입문' 카테고리의 다른 글
| 베이즈 정리 (0) | 2022.11.23 |
|---|---|
| 연관성 척도 (0) | 2022.11.08 |
| 특이값과 Z-Score (0) | 2022.09.30 |
| 변동성 척도(4분위수를 배운 이유) (0) | 2022.09.18 |
| 중심위치 척도... (0) | 2022.09.15 |



