분할
$ A $와 $ A^{c} $ 은 서로 겹치지 않는다. 즉 상호배반이며 합사건에 대해서는 표본공간을 이룬다.
즉 표본공간이 두 개의 사건 $ A $와 $A^{c} $에 의해서 분할된다고 표현된다.
즉 {$ A,A^{c} $} 는 표본공간의 분할이다.
분할에 대한 정리는 다음과 같다.
사건들의 모임 {$ A_1,A_2,\cdots,A_n $}이 표본공간의 분할이 되기 위해서는 다음을 만족한다.
1. $ A_i \cap A_j = \varnothing $
$ \forall i\neq j$, 즉 각각의 사건들이 상호배반이여야 한다
2. $ \bigcup_{i=1}^{n}{A_i}=\Omega $
즉 모든 사건들의 합사건은 표본공간을 이루어야 한다
총확률의 법칙
분할을 이용한 총확률에 대해 알아보자
이 그림을 통해서 B의 확률은 어떻게 나타낼 수 있을지 생각해보자
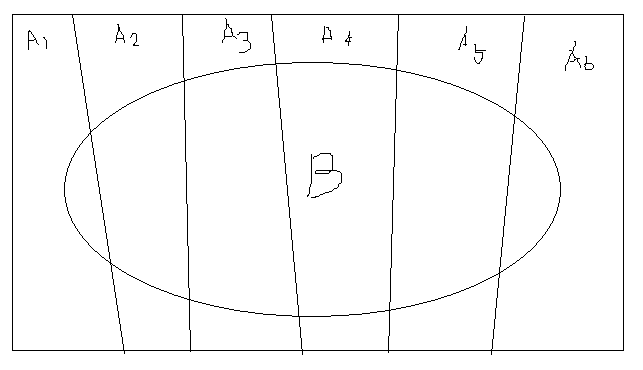
$ P(B)=P(A_1\cap B)+P(A_2\cap B)+\cdots+P(A_n\cap B) $으로 나타낼 수 있다.
그렇다면 우리가 앞서 배운 곱셈공식을 이용해보자
하나씩 적용한다면 다음과 같다.
$ P(A_1\cap B) = P(A_1)P(B|A_1) $
$ P(A_2\cap B) = P(A_2)P(B|A_2) $
$ \cdots $
$ P(A_n\cap B) = P(A_n)P(B|A_n) $
위의 수식을 한꺼번에 더하여 정리하면
이것은 B에 대한 총확률의 법칙이다.
$ P(B) = P(A_1)P(B|A_1) + P(A_2)P(B|A_2) + \cdots + P(A_n)P(B|A_n) $
$ = \sum_{i=1}^{n}P(A_i)P(B|A_i) $
흠...그렇다면
총확률의 법칙은 어디다가 써먹을까?
바로 이 글의 핵심 베이즈 정리에 써먹는다.
베이즈 정리
{$ A_1,A_2,\cdots,A_n $}이 표본공간의 분할일 때 임의의 사건 B에 대하여,
$A_k$의 조건부확률은 다음과 같다
$ P(A_k|B)=\frac{P(A_k\cap B)}{P(B)}=\frac{P(A_k)P(B|A_k)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)} $
위의 그림을 예시로 $ P(A_3|B) $를 알고싶다면 베이즈 정리를 이용하여 다음과 나타낼 수 있다.
$ P(A_3|B)=\frac{P(A_3)P(B|A_3)}{P(A_1)P(B|A_1)+\cdots P(A_6)P(B|A_6)} $
이 글을 마치며 확률에 대한 내용을 끝내고 확률분포로 넘어가는 내용을 추후 작성하겠다.
'Statistics > 확률론' 카테고리의 다른 글
| 6. 이산형 확률변수(베르누이 분포) (0) | 2023.11.14 |
|---|---|
| 5. 확률변수, 그리고 확률 질량 함수(PMF) (1) | 2023.11.14 |
| 3. 조건부 확률 (0) | 2023.10.15 |
| 2. 용어, 가법정리 (0) | 2023.10.11 |
| 1. 확률의 공리 (0) | 2023.10.11 |